papers
Updated aug-25. See my Google Scholar page for a more up-to-date list.
-
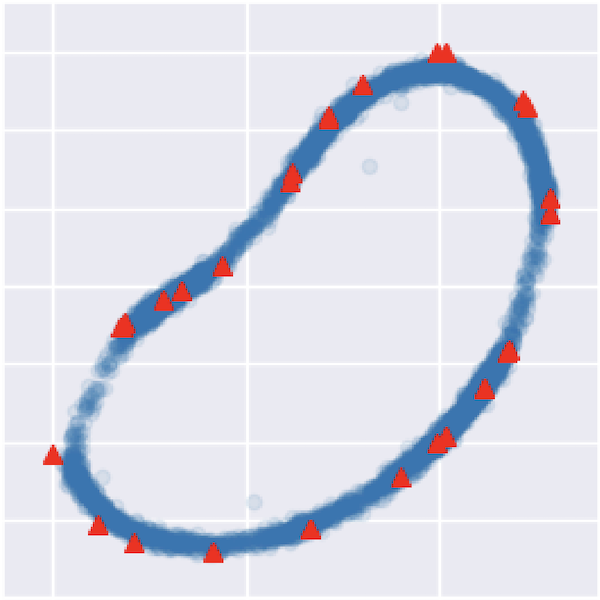 Diffusion Models and the Manifold Hypothesis: Log-Domain Smoothing is Geometry AdaptiveDraft available on request 2025
Diffusion Models and the Manifold Hypothesis: Log-Domain Smoothing is Geometry AdaptiveDraft available on request 2025Diffusion models have achieved state-of-the-art performance, demonstrating remarkable generalisation capabilities across diverse domains. However, the mechanisms underpinning these strong capabilities remain only partially understood. A leading conjecture, based on the manifold hypothesis, attributes this success to their ability to adapt to low-dimensional geometric structure within the data. This work provides evidence for this conjecture, focusing on how such phenomena could result from the formulation of the learning problem through score matching. We inspect the role of implicit regularisation by investigating the effect of smoothing minimisers of the empirical score matching objective. Our theoretical and empirical results confirm that smoothing the score function—or equivalently, smoothing in the log-density domain—produces smoothing tangential to the data manifold. In addition, we show that the manifold along which the diffusion model generalises can be controlled by choosing an appropriate smoothing.
-
 Implicit Regularisation in Diffusion Models: An Algorithm-Dependent Generalisation AnalysisarXiv preprint 2025
Implicit Regularisation in Diffusion Models: An Algorithm-Dependent Generalisation AnalysisarXiv preprint 2025The success of denoising diffusion models raises important questions regarding their generalisation behaviour, particularly in high-dimensional settings. Notably, it has been shown that when training and sampling are performed perfectly, these models memorise training data – implying that some form of regularisation is essential for generalisation. Existing theoretical analyses primarily rely on algorithm-independent techniques such as uniform convergence, heavily utilising model structure to obtain generalisation bounds. In this work, we instead leverage the algorithmic aspects that promote generalisation in diffusion models, developing a general theory of algorithm-dependent generalisation for this setting. Borrowing from the framework of algorithmic stability, we introduce the notion of score stability, which quantifies the sensitivity of score-matching algorithms to dataset perturbations. We derive generalisation bounds in terms of score stability, and apply our framework to several fundamental learning settings, identifying sources of regularisation. In particular, we consider denoising score matching with early stopping (denoising regularisation), sampler-wide coarse discretisation (sampler regularisation) and optimising with SGD (optimisation regularisation). By grounding our analysis in algorithmic properties rather than model structure, we identify multiple sources of implicit regularisation unique to diffusion models that have so far been overlooked in the literature.
-
We establish disintegrated PAC-Bayesian generalisation bounds for models trained with gradient descent methods or continuous gradient flows. Contrary to standard practice in the PAC-Bayesian setting, our result applies to optimisation algorithms that are deterministic, without requiring any de-randomisation step. Our bounds are fully computable, depending on the density of the initial distribution and the Hessian of the training objective over the trajectory. We show that our framework can be applied to a variety of iterative optimisation algorithms, including stochastic gradient descent (SGD), momentum-based schemes, and damped Hamiltonian dynamics.
-
 Cognitive Infrastructures: Conjectural Explorations of AI as a Physical Actor in the WildJournal for the Philosophy of Planetary Computation, Antikythera 2025
Cognitive Infrastructures: Conjectural Explorations of AI as a Physical Actor in the WildJournal for the Philosophy of Planetary Computation, Antikythera 2025In this paper, we explore several conjectural scenarios for the development of artificial intelligence as a force animating the physical infrastructures of everyday life. We do so by foregrounding the real and potential co-evolution of natural and machine intelligence in relation to one another. The proposals are diverse and developed semi-independently in the context of a one month intensive research studio. However, if imagined as a single integrated speculation described from different vantage points, it might be as follows: the executable embedding of a society of digital twins of brain organoids that run in slow computational time by driving artificial epidermal mediated distributed organs, are in turn part of xenomorphic biohybrid robotic phenotypes that produce various levels of nested minimum viable interiorities with which human-users deploy inverted embedding visualizations to learn new game theoretic dynamics through adaptive anti-transitivity, shifting asymmetries of mutual mind modeling, and carefully calibrated novelty-inducing disalignments. The composite assemblage would be fixed in a long-term durational imprint backed up on a highly durable substrate for long-term decoding.
-
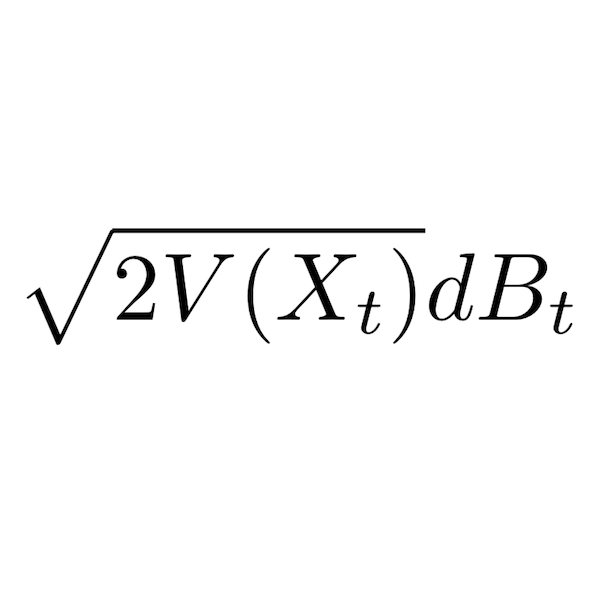
We analyze the complexity of sampling from a class of heavy-tailed distributions by discretizing a natural class of Itô diffusions associated with weighted Poincaré inequalities. Based on a mean-square analysis, we establish the iteration complexity for obtaining a sample whose distribution is ϵ close to the target distribution in the Wasserstein-2 metric. In this paper, our results take the mean-square analysis to its limits, i.e., we invariably only require that the target density has finite variance, the minimal requirement for a mean-square analysis. To obtain explicit estimates, we compute upper bounds on certain moments associated with heavy-tailed targets under various assumptions. We also provide similar iteration complexity results for the case where only function evaluations of the unnormalized target density are available by estimating the gradients using a Gaussian smoothing technique. We provide illustrative examples based on the multivariate t-distribution.
-
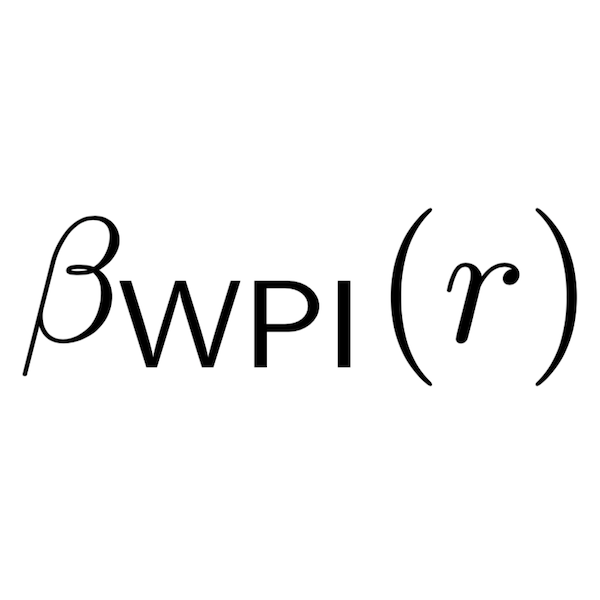 Towards a Complete Analysis of Langevin Monte Carlo: Beyond Poincaré InequalityIn COLT 2023
Towards a Complete Analysis of Langevin Monte Carlo: Beyond Poincaré InequalityIn COLT 2023Langevin diffusions are rapidly convergent under appropriate functional inequality assumptions. Hence, it is natural to expect that with additional smoothness conditions to handle the discretization errors, their discretizations like the Langevin Monte Carlo (LMC) converge in a similar fashion. This research program was initiated by Vempala and Wibisono (2019), who established results under log-Sobolev inequalities. Chewi et al. (2022a) extended the results to handle the case of Poincaré inequalities. In this paper, we go beyond Poincaré inequalities, and push this research program to its limit. We do so by establishing upper and lower bounds for Langevin diffusions and LMC under weak Poincaré inequalities that are satisfied by a large class of densities including polynomially-decaying heavy-tailed densities (i.e., Cauchy-type). Our results explicitly quantify the effect of the initializer on the performance of the LMC algorithm. In particular, we show that as the tail goes from sub-Gaussian, to sub-exponential, and finally to Cauchy-like, the dependency on the initial error goes from being logarithmic, to polynomial, and then finally to being exponential. This three-step phase transition is in particular unavoidable as demonstrated by our lower bounds, clearly defining the boundaries of LMC.
-
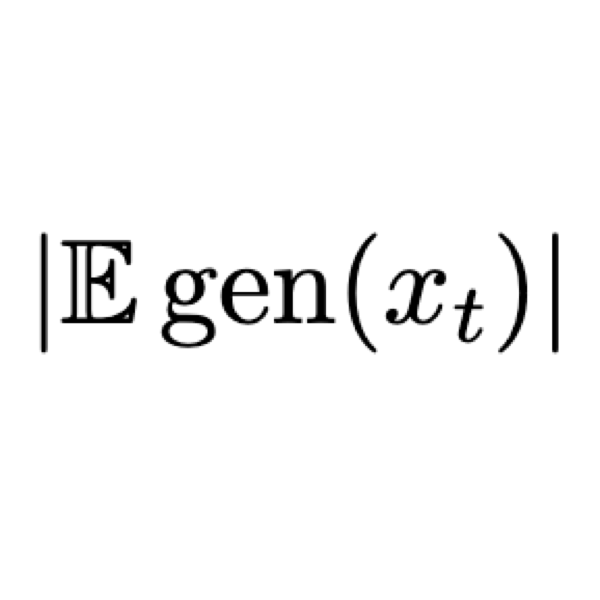
We establish generalization error bounds for stochastic gradient Langevin dynamics (SGLD) with constant learning rate under the assumptions of dissipativity and smoothness, a setting that has received increased attention in the sampling/optimization literature. Unlike existing bounds for SGLD in non-convex settings, ours are time-independent and decay to zero as the sample size increases. Using the framework of uniform stability, we establish time-independent bounds by exploiting the Wasserstein contraction property of the Langevin diffusion, which also allows us to circumvent the need to bound gradients using Lipschitz-like assumptions. Our analysis also supports variants of SGLD that use different discretization methods, incorporate Euclidean projections, or use non-isotropic noise.
-
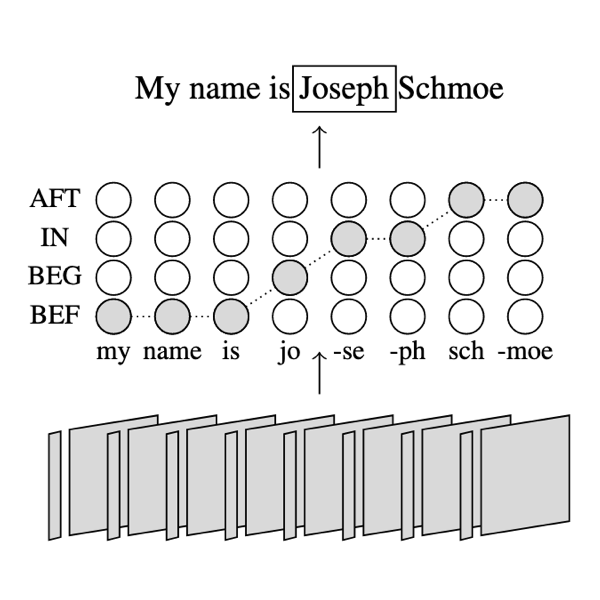 Span-ConveRT: Few-shot Span Extraction for Dialog with Pretrained Conversational RepresentationsIn ACL 2020
Span-ConveRT: Few-shot Span Extraction for Dialog with Pretrained Conversational RepresentationsIn ACL 2020We introduce Span-ConveRT, a light-weight model for dialog slot-filling which frames the task as a turn-based span extraction task. This formulation allows for a simple integration of conversational knowledge coded in large pretrained conversational models such as ConveRT (Henderson et al., 2019). We show that leveraging such knowledge in Span-ConveRT is especially useful for few-shot learning scenarios: we report consistent gains over 1) a span extractor that trains representations from scratch in the target domain, and 2) a BERT-based span extractor. In order to inspire more work on span extraction for the slot-filling task, we also release RESTAURANTS-8K, a new challenging data set of 8,198 utterances, compiled from actual conversations in the restaurant booking domain.